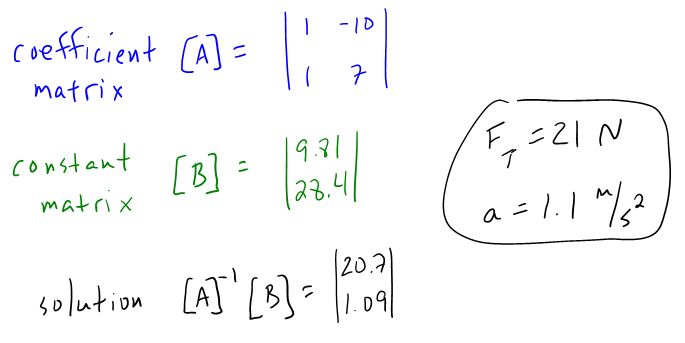Introduction

While it is sometimes useful to imagine a situation without friction, on Earth, friction is ever present. This page works through a number of examples that require the consideration of friction.

Example - One block hanging

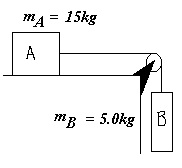
A wooden block, A, rests on a wooden table and is attached to another block, B, with a massless rope through a pulley as shown in the diagram below. What is the force of static friction keeping block A from sliding across the table, if the coefficient of static friction is μ_s = 0.40?

Solution

Draw a free body diagram of each block separately.

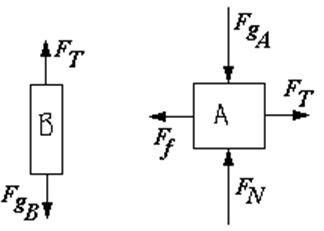
Since the system is at rest, we know that for each block, ΣF = 0 . We also know that the tension force, F_T, is the equal, but opposite, on each block. We solve for the forces on block B first, then for the frictional force on block A.

Example - Hanging block too heavy

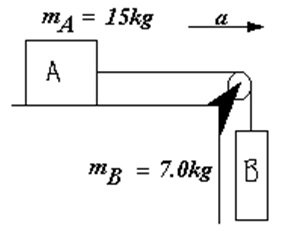
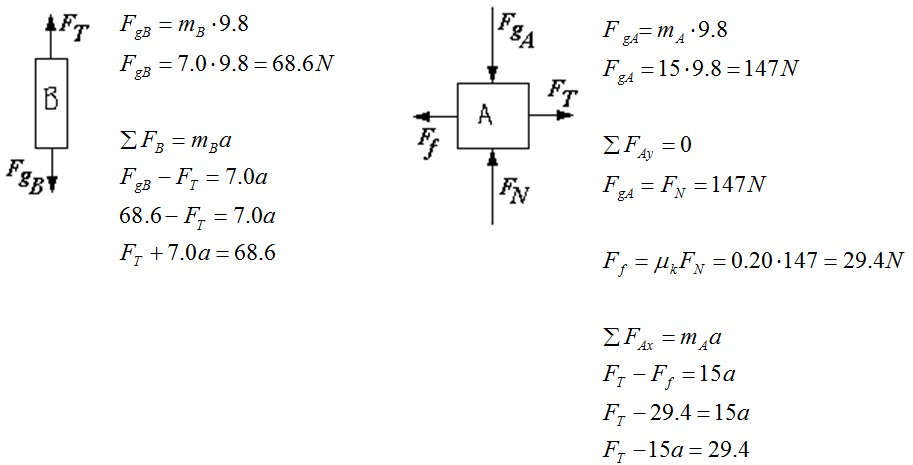
A wooden block, A, slides on a wooden table and is pulled by another block, B, with a massless rope through a pulley as shown in the diagram below.

1. What is the force of kinetic friction retarding block A as it slides across the table, if the coefficient of kinetic friction is μ_k = 0.20?
2. What is the acceleration of the system?

Solution

Draw a free body diagram of each block separately then solve for two equations in F_T and a.

With two equations and two unknowns, you need to solve the system of equations. This is done below using a matrix solution.

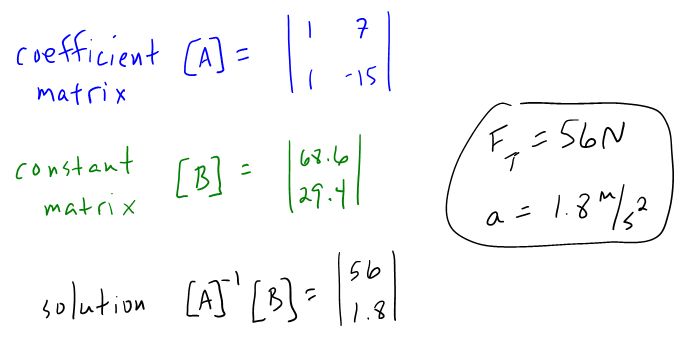
Example - Rough ramp

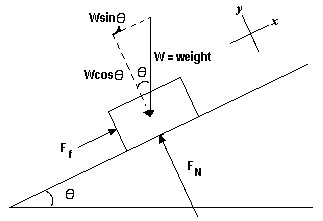
A 12kg wooden block is set on a 25° wooden inclined plane with a coefficient of static friction, μ_s=0.40 and a coefficient of kinetic friction μ_k = 0.20 between the two.

1. Will the block slide down the plane?
2. What is the force of friction retarding the block?
3. If the block slides, what is the block’s acceleration?

Solution

Solve the x and y components separately. Look to see if the x-component of the weight is greater than the maximum static friction force possible. If it is, the block will slide down the ramp.

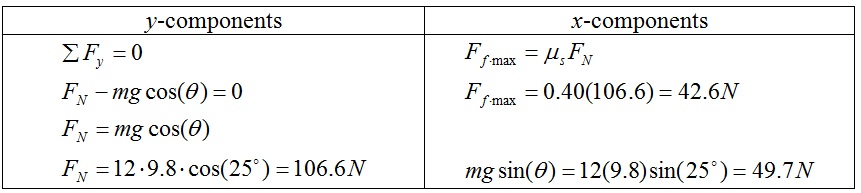
The x-component of the weight (49.7N) is greater than the possible static friction (42.6N).  The block will slide down the ramp.

Solve now for the kinetic friction retarding the block.

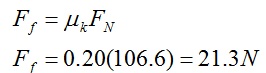
Solve for the acceleration of the block using Newton’s second law.

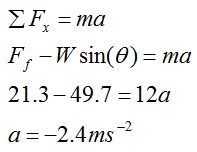
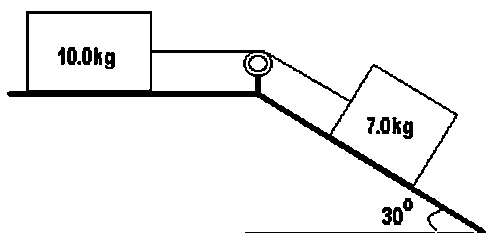
Example - Connected blocks on a rough ramp

As shown in the diagram below, an object m₁=10.0kg is connected by a massless unstretchable rope to another object m₂=7.0kg which rests on a 30° incline. The coefficient of kinetic friction between the objects and the surfaces is 0.10. Determine

1. the rate of acceleration of the system
2. the tension in the rope that connects the two objects.

Solution

Draw a free body diagram of each block separately then solve for two equations in F_T and a.

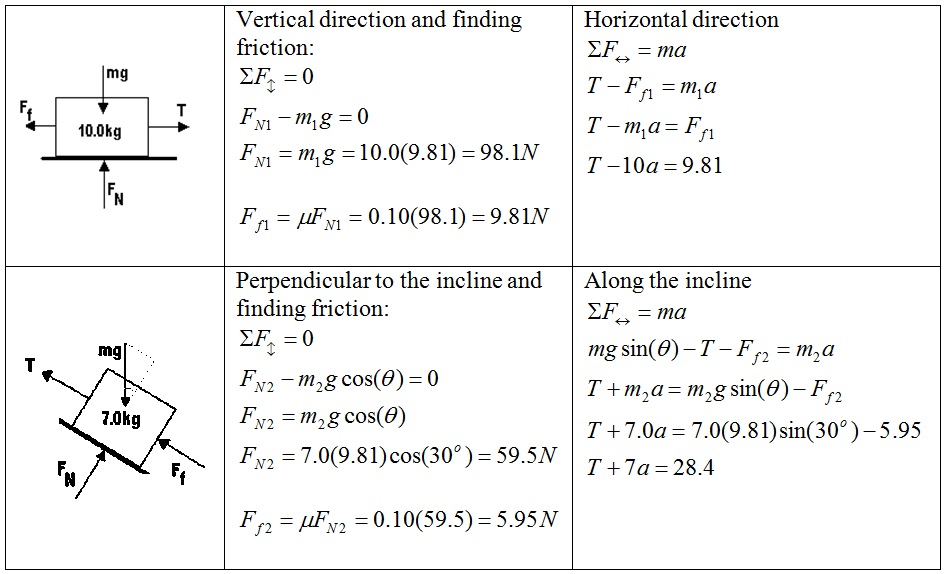
With two equations and two unknowns, you need to solve the system of equations. This is done below using a matrix solution.