Series Circuits

A series circuit is one where resistors are placed one after the other on a single path for the current. The current is forced to move through one resistor before passing into the next - there is only one path for the current.

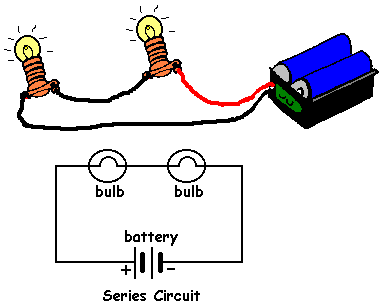
The most pratical use for series circuits is when adding a fuse to a circuit. Fuses are devices that either burn out or open when the current through the circuit gets too high. They prevent a fire or the destruction of expensive electrical equipment by a overly large current.

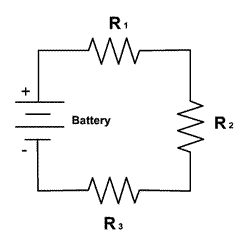
adding resistors in series

In series, resistors add just like numbers.

The current, I_total, that leaves the battery can be found using Ohm's Law if the battery voltage, V_total is known.

The voltage drop across each resistor can be calculated using Ohm's Law once the total current is known. For example, the voltage drop across R₁ can be calculated as shown below:

The sum of all the voltage drops in a series circuit should equal the total voltage applied across the circuit.

Example - Who is the line leader?

• Question
• Answer

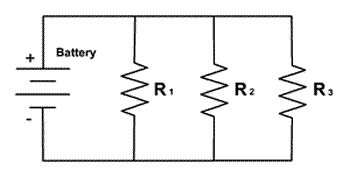
Parallel Circuits

A parallel circuit is one where each resistor has its own connection to the voltage source. The current splits off and flows separately to each resistor in parallel. All theses individual currents then meet back up to return to the voltage source.

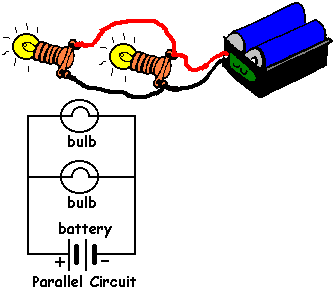
Most household wiring (excpet for fuses as explained earlier) is done in parallel. In this way, if one light bulb blows the rest of the house is still functional.

adding resistors in parallel

In parallel, we use an inverse rule for adding resistors.

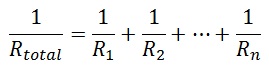
The current, I_total, that leaves the battery can be found using Ohm's Law if the battery voltage, V_total is known.

The current through each resistor can be calculated using Ohm's Law knowing that each resistor is powered by the same voltage, V_total. For example, the current through R₁ can be calculated as shown below:

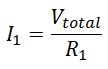
The sum off all the currents through each bracnh should add up to the current leaving or entering the battery.

Example - Drinking from many straws

• Question
• Answer

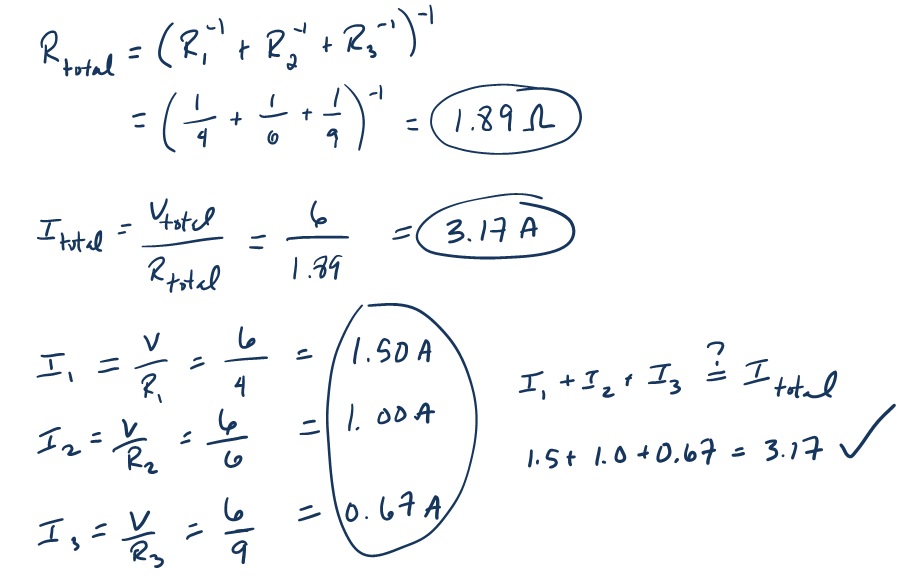
Series-Parallel Circuits

Most real circuits have some resistors that are in series and some resistors in parallel. The trick to solving these circuits is to apply the series and parallel math rules in just the correct way.

Terminal Voltage

A dry cell can be represented as and potential difference, ε, in series with an internal resistance, r, as shown in the diagrams below.

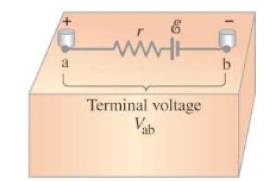
This internal resistance is a property of the chemicals and materials that make up the battery. The value of the internal resistance is not constant, but during normal operations before the battery is near depletion, it can be modeled mathematically as constant.

The internal resistance does affect the voltage that the battery supplies. When the battery is not connected to the circuit (no current is flowing from the battery) the voltage measured across its terminals - the terminal voltage, V - is equal to the internal potential difference, ε.

However, when the battery is in use, when there is a current flowing through r, then there is a voltage drop inside the battery equal to Ir. This lowers the terminal voltage that the battery actually supplies to the circuit. The terminal voltage can be calculated with the following formula:

Potential Dividers Circuits (Voltage Dividers)

A potential diveder circuit allows you to take a supply voltage that may be too high and lower it to a value more appropriate for the component being used.

The basic design of the circuit is shown in the diagram below.

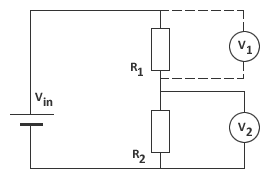
The supply voltage, V_in, is stepped down by the first resistor (R₁), so that the load (R₂) is run by the remaining voltage:

V₂ = V_in - V₁

A more useful formula for calculating V₂ is given below.

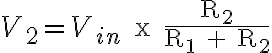
Replacing R2 with a Light dependent resistor (LDR)

The LDR is a component that has a resistance that changes when light falls on it. As the intensity of the light is increased so the resistance of the LDR falls. If the LDR is connected as part of a potential divider as shown in the diagram then as the light level is increased its resistance falls and the proportion of the input voltage dropped across it will also fall. So in the light V₂ is low and in the dark V₂ is high.

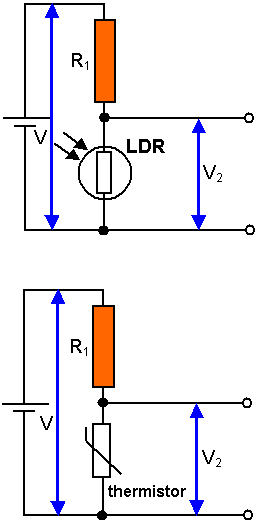
Replacing R2 with a thermistor

Something very similar happens if R₂ is replaced by a thermistor. As the temperature of the thermistor rises its resistance falls and so the voltage dropped across it falls. When the thermistor is hot V₂ is low and when the thermistor is cold V₂ is high.

Practice

16. Three resistors are in series with a 12V battery. The resistors have values of R₁=100 Ω, R₂=60Ω, and R₃=75Ω. Find
    1. The total resistance in the circuit.
    2. The current through each resistor.
    3. The voltage drop across each resistor.
17. Three resistors are in parallel with a 12V battery. The resistors have values of R₁=100 Ω, R₂=60Ω, and R₃=75Ω. Find
    1. The total resistance in the circuit.
    2. The current through each resistor.
    3. The voltage drop across each resistor.
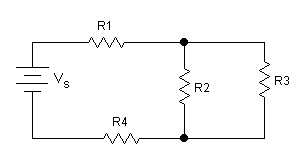18. Four resistors are arranged in a circuit as shown in the diagram to the right. The resistors have values of R₁=100 Ω, R₂=60Ω, R₃=75Ω, and R₄=125Ω. The battery has a voltage of 60V. Find
    1. the total resistance
    2. the total current
    3. the voltage drop across each resistor
    4. the current through each resistor.
19. Six resistors are arranged in a circuit as shown in the diagram to the right. The resistors have values of R₁=100 Ω, R₂=60Ω, R₃=75Ω, R₄=125Ω, R₅=80Ω, and R₆=25Ω. The battery has a voltage of 120V. Find
    1. the total resistance
    2. the total current
    3. the voltage drop across each resistor
    4. the current through each resistor.

click here for solutions